Ik moet toch nog het één en ander opzoeken vooraleer ik me toch een gedacht kan vormen hoe dat nu zit voor de gevoeligheid van de LNA. Ruis is in normale omstandigheden altijd aanwezig . Het hoeveel ervan in mijn frequentiegebied is hetgene is toch zou moeten te weten komen. Mijnheer Nyquist en Johnson en met bijdrage van Mijnheer Boltzmann hebben dit uitvoerig bestudeerd.
Uit wiki : Noise
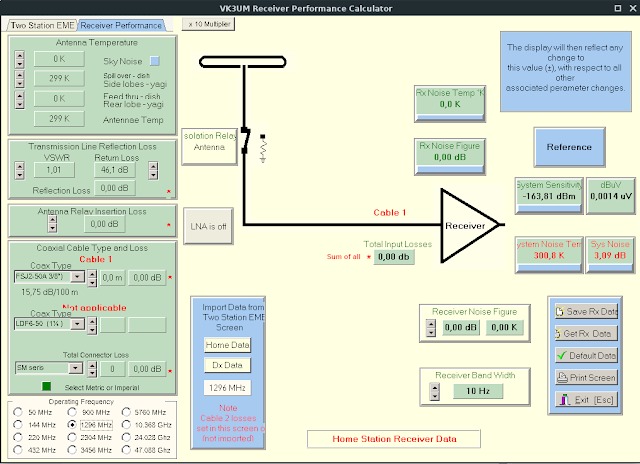
Blijven we bij de extreme smalle bandbreedte ( BB ) van 10 Hz , dan zou een weerstand bij die BB een ruisvermogen opwekken van - 164 dBm, bij 300°K.
Hierbij een berekening ( simulatie) waarbij ik de system noise temp ingesteld heb op 300°K en de BB op 1 Hz . Alle andere faktoren zijn op 0 ingesteld.
Hierbij is de uitkomst: -173.82 dBm.
Dit komt dus overeen met de tabel van wiki . Dit bevestigt dus de goeie berekening van dit programma en kunnen we dit met gerust gemoed verder gebruiken.
Hetzelfde voor BB van 10 Hz, waarden kloppen ook.
Nu wordt het interessant.
De 300°K is een parameter voor het ruisvermogen . Echter de parabool "ziet" geen 300°K maar een veel lagere temperatuur afhankelijk hoe hij kijkt .
Daarvoor zijn er in te vullen velden voorzien om dit te compenseren en hiermee wordt de gevoeligheid van het ontvangstsysteem verbetert.
Dit is dus een pluspunt. Volgende maal simuleer ik de NF en Gain van de eerste préamp , de LNA dus , en de invloed ervan op onze gevoeligheid.
Geen opmerkingen:
Een reactie posten